Statistictionary | Blockchain Security
Blockchain technology was first described in the 1990s; the aim was to timestamp digital documents so that it was not possible to backdate them. However, the technology gained popularity with its application in Bitcoin in 2009.
Blockchain is a distributed, decentralized, public ledger; it’s the record-keeping technology behind the Bitcoin network. As the name indicates, a blockchain is a chain of information-containing blocks. Once data has been stored inside a blockchain, it becomes very difficult to make unauthorized changes to it. Blockchain’s distributed and decentralized nature have made it a very popular technology, although it still faces the same main issues as any technology, namely usability, security, and trustworthiness.[1]
Is Blockchain Secure?
Each new user transaction creates a new block in the chain and the blockchain is updated in its network of thousands (or millions) of computers. This distribution of information across such a large network makes it very hard to manipulate. If someone wishes to alter a particular transaction in a block, they will need to manipulate copies of the blockchain in more than 50% of the network’s computers. This defines the “distributed” ledger property of blockchain.
Public-Key Cryptography
Despite all the transaction information on a blockchain being public, personal information for any user is limited to their digital signature or username. Each participant has a “wallet” through which they run all their transactions, and each wallet is equipped with two different cryptographic keys: a public key and a private key. The public key is what appears in the transaction ledger, tagging the transaction to the user. However, the user needs the private key to withdraw their bitcoins. The public key is derived from the private key using complex algorithms, and the process is almost irreversible – i.e. you cannot generate a user’s private key from his public key, hence ensuring the safety of the user’s wallet.[2]
The mathematics behind blockchain is highly complex and relies on Elliptical curve cryptography to ensure that a transaction is secure. The members make use of the Elliptic curve digital signature algorithm (ECDSA) each time they make a transaction.
General Equation [3]
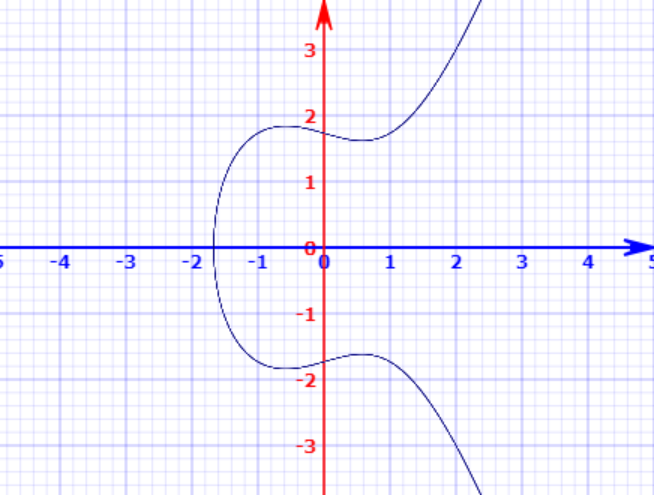
Elliptic curve: y^2 = x^3+ax+b
For Bitcoin: y^2 = x^3+7 (a=0 and b=7)
One of the properties of the elliptic curve is that a non-vertical line passing through two points on the curve would also intersect on a third point.
Figure 1: Elliptic Curve [3]
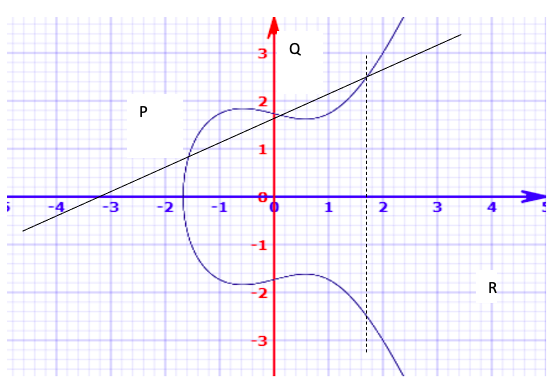
If you want to add two points on an elliptic curve, you first draw a line through the two points. When you find the point where the line intersects the curve for the third time, you reflect the third point on the x-axis; this will give you the addition of the first two points.
Figure 2: Elliptic Curve- Addition of two points [3]
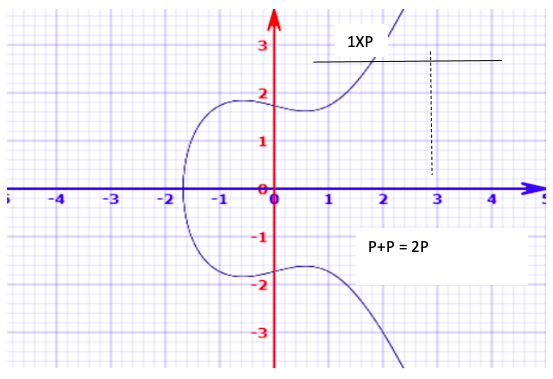
To do Elliptic curve cryptography efficiently, rather than the aforementioned addition of random points, we specify a base point on the curve and only add that point to itself.
If we have an initial point P, the reflected point will be 2P. We can continue to compute 3P, 4P, and so on. If we think about it, how many steps will it take to compute 10P?
In general, 10P = P+P+P+P+P+P+P+P+P+P, i.e. a 9-step operation.
However, since the property nP+rP = (n+r)P holds, we can also compute 10P in this manner:
1P+1P = 2P
2P+2P = 4P
4P+4P = 8P
2P+8P = 10P
Figure 3: Elliptic Curve- Addition of base points [3]
Accordingly, how many steps would be required to compute xP, where ‘x’ is a random 256-bit integer that ranges from 0 to a very high integer?
It turns out computing xP would never require more than 510 step operations.
Since elliptic curve cryptography does not support a ‘division’ function, in the equation X = xP we cannot calculate ‘x’ given ‘X’. It makes sense to assign ‘x’ to be a private key and ‘X’ to be a public key. Your private key would then be a 256-bit integer, whereas your public key would be the x and y coordinates on the elliptic curve. It would then be computationally impossible to arrive at your private key from your public key.
Conclusion
We can safely say that the mathematics involved in the generation of security keys is very complex and is not trivial. We have also seen that it is easier to arrive at a user’s public key from their private key than vice-versa. ECDSA is the underlying essence of how all blockchain applications work. [3]
References