Thriving Traction | Bayesian Hyperparameter Optimization

Introduction

Hyperparameter tuning is the process of finding the best subset of hyperparameters for a given problem. Simply put, we use this tuning to figure out if a tree depth of 12 is better than a depth of 20 or if 100 epochs will do instead of 1,000 epochs.

Hyperparameter tuning is a crucial part of the model training process and can lead to a roughly 10% improvement in accuracy if done right. There are different techniques a data scientist uses to tune the hyperparameters of a model:

1. Manual tuning: A good fast way to tune hyperparameters is to start with parameters that work on similar problems, datasets, and model structures and optimize these parameters. This method, however, does not guarantee good results.
2. Grid Search: This involves iterating over all possible hyperparameter values. As you can imagine, this method gets out of hand as the number of hyperparameters to tune increases.
3. Random Search: This is one of the best approaches to hyperparameter tuning and has been used extensively. But it takes a long time to reach the optimal point.
4. Bayesian Hyperparameter Optimization: This method enables you to learn from previous tuning runs and reduce search space. This greatly decreases the time required to find the optimal (or nearly optimal) parameters.

From the description above, Bayesian optimization seems to be the best way to tune hyperparameters. What exactly is it?

Bayesian Hyperparameter Optimization Explained

On a high level, Bayesian hyperparameter optimization creates a surrogate model ^[1] for the model we want to tune. This model predicts the original model’s score for a given set of hyperparameters. The surrogate model runs much faster than training your machine learning model, so the whole process of tuning is quicker. The main idea is to use information from all previous evaluations, not just the current one.^[2] Thus, this procedure leads to better hyperparameters with much fewer model training iterations. We can see below the results Bergstra et al. got when they used Bayesian optimization to tune their hyperparameters. ^[3]

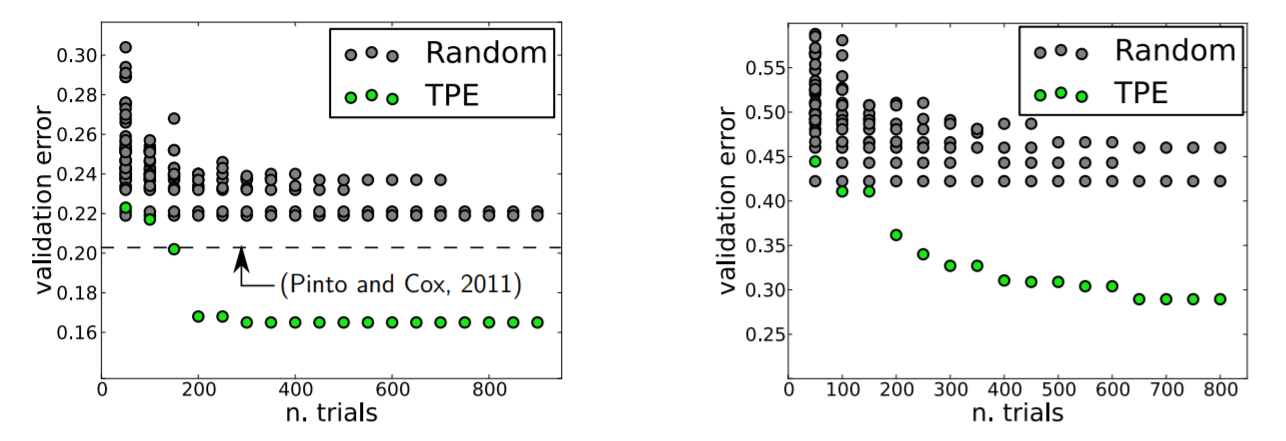
Figure 1: Validation error on two datasets using random search in grey and Bayesian optimization in green (using Tree Parzen Estimator). ^[4]

We use Bayesian methods to create the surrogate model and then sample a point from the posterior distribution that we think will give us the highest score. We then run the original model with these hyperparameters and update our surrogate model. We keep on repeating this process until we reach the specified number of iterations.

As you can imagine, the surrogate model gets better with each iteration of the original model. This ensures that we look only in the neighborhood of the best possible hyperparameters. We can see Bayesian optimization achieve this in the images below:

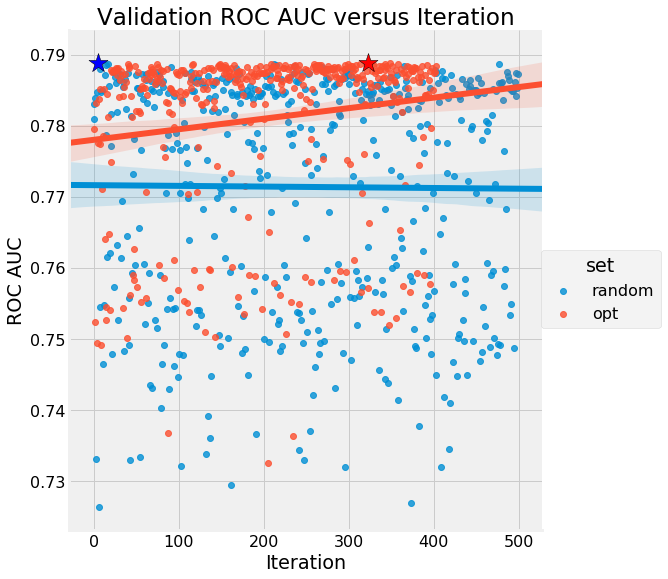
Figure 2 (a): Validation AUC using random search and Bayesian optimization. There is a clear uptrend in the performance of the Bayesian optimization method. ^[5]

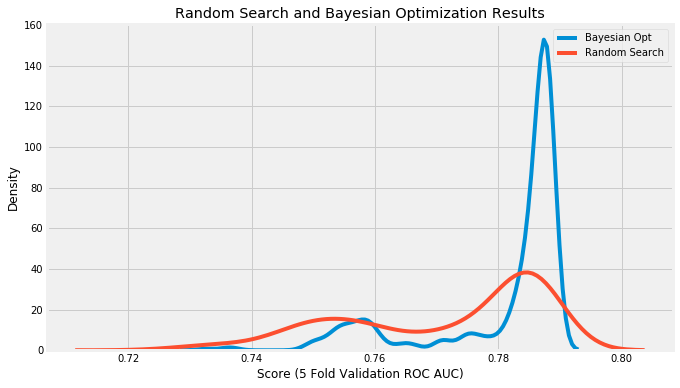
Figure 2 (b): AUC vs. the hyperparameters tried for the same dataset as (a). As you can see, the Bayesian optimization had its search centered around the best hyperparameters, whereas random search was simply lucky in finding the hyperparameters. ^[5]

If training your machine learning model is expensive in terms of money, resources, or time, Bayesian optimization is the way to go. However, there are a few things to note about Bayesian optimization:

1. It is helpful only when training your machine learning model is slower than the acquisition function you use. If training your model is faster, use random search.
2. Bayesian optimization struggles with high-dimensionality problems; it might not be the best approach to hyperparameter tuning if you have dozens of hyperparameters.

You can start implementing Bayesian hyperparameter tuning in your projects using either Hyperopt ^[6] or Bayesian Optimization ^[7] and experience the results with little modification.

References

1. https://towardsdatascience.com/a-conceptual-explanation-of-bayesian-model-based-hyperparameter-optimization-for-machine-learning-b8172278050f

2. Snoek, Jasper, Hugo Larochelle, and Ryan P. Adams. “Practical Bayesian optimization of machine learning algorithms.” In Advances in neural information processing systems, pp. 2951-2959. 2012.

   (https://papers.nips.cc/paper/4522-practical-bayesian-optimization-of-machine-learning-algorithms.pdf)

3. Source: Bergstra, James, Daniel Yamins, and David Cox. “Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures.” In International conference on machine learning, pp. 115-123. 2013.

   (http://proceedings.mlr.press/v28/bergstra13.pdf)

4. Bergstra, James S., Rémi Bardenet, Yoshua Bengio, and Balázs Kégl. “Algorithms for hyper-parameter optimization.” In Advances in neural information processing systems, pp. 2546-2554. 2011.

   (https://papers.nips.cc/paper/4443-algorithms-for-hyper-parameter-optimization.pdf)

5. Source:

   https://www.kaggle.com/willkoehrsen/model-tuning-results-random-vs-bayesian-opt

6. Hyperopt:

   https://hyperopt.github.io/hyperopt/
   

7. Bayesian Optimization:

   https://www.irit.fr/~Didier.Dubois/Papers1208/possibility-EUSFLAT-Mag.pdf

8. https://mlconf.com/blog/lets-talk-bayesian-optimization/
   

Subscribe to BrainWave